[자동제어] 수업을 들을때 연립방정식과 고차방정식을 해결해야 하는 경우가 종종 있습니다.
보통 상태공간에서 문제를 해결할때 연린방정식을,
그리고 전달함수에서 특성방정식의 근을 구할때 고차방정식을 사용합니다.
따라서 이번에는 파이썬코드를 통해 연립방정식 해법과 고차방정식 해법에 대해 알아보도록 하겠습니다.
x와y에 대한 연립방정식 해결하기
문제)
\begin{align*}
2x+y &= 8\\
3x-2y &= -5\\
\end{align*}
위 연립방정식에서 x와 y의 값을 구하라.
이를 파이썬에서 넘파이를 써서 해결하기 위해 우선 행렬식 형태로 바꿔야 한다.
$$A=\begin{bmatrix}
0 & 1 & 2\\
3 & 4 & 5\\
6 & 7 & 8
\end{bmatrix}
$$
$ A = \begin{bmatrix}
0 & 1 & 2\\
3 & 4 & 5\\
6 & 7 & 8
\end{bmatrix} $
<!-----------------------------------------------
$ A = \begin{bmatrix}
1 & 2\\
3 & 4
\end{bmatrix} $
\begin{bmatrix}
2 & 1 \\
3 & -2 \\
\end{bmatrix}^{-1}\bullet \begin{bmatrix}
8 \\
-5 \\
\end{bmatrix}
$ A = \begin{bmatrix}
1 & 2\\
3 & 4
\end{bmatrix} $
\begin{align*}
x&=y & w &=z & a&=b+c\\
2x&=-y & 3w&=\frac{1}{2}z & a7=b\\
-4 + 5x&=2+y & w+2&=-1+w & ab&=cb
\end{align*}
$ y = ae^x $
$ A = \begin{bmatrix}
1 & 2\\
3 & 4
\end{bmatrix} $
$ x = \frac{-b \pm \sqrt{b^2 - 4ac} }{2a} $
여기서
x
는 이차방정식의 해이다.
$ \begin{align*}
z &= (x + y)^2\\
&= x^2 + 2xy + y^2
\end{align*} $
$ y = \sum_{i = 1}^{10}x_i $
----------------------------->
코드)
import numpy as np
# 연립방정식의 계수 행렬
A = np.array([[2, 1],
[3, -2]])
# 연립방정식의 상수 벡터
B = np.array([8, -5])
# 연립방정식 풀기
solution = np.linalg.solve(A, B)
print(f"The solution is x = {solution[0]}, y = {solution[1]}")
결과)
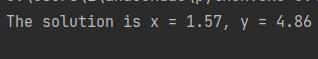
4차 방정식 해결하기
import numpy as np
# 방정식의 계수를 정의
coefficients = [1, 2, 3, 4] #요소의 개수가 4라는 것은 0차항부터 3차항까지 해서 총 4차방정식임을 의미합니다.
# numpy.roots() 함수를 사용하여 방정식의 해를 계산
solutions = np.roots(coefficients)#방저식의 해는 배열로 저장됩니다.
# 해 출력
print("방정식의 해:", solutions)
결과>

'자료구조 > numpy 자료구조' 카테고리의 다른 글
| Numpy - where() 사용 방법 (1) | 2023.03.25 |
|---|---|
| numpy flatten() 함수, 1차원 배열로 변환(평탄화) (1) | 2023.03.25 |
| numpy hstack, vstack 함수 (배열 연결) (2) | 2023.03.25 |
| np.linspace와 np.arange의 차이에 대해 알아보자! (1) | 2023.03.25 |


댓글